Para hallar el desplazamiento de la moto debemos tener en cuenta que la velocidad varía linealmente con el tiempo y en general el desplazamiento para un movimiento rectilíneo es:  (3). (3).
Teniendo en cuenta que en el gráfico de valor de velocidad en función del tiempo, el área bajo la curva es numéricamente al desplazamiento realizado, podemos encontrar la solución
Si calculamos la velocidad media en este movimiento obtenemos que es igual a la semisuma de los valores inicial y final de velocidad en el intervalo dado.
 (4) entonces el desplazamiento puede expresarse como:
(El profesor debe saber que si somos consecuente con las cifras significativas del problema el resultado debe expresarse como, 2,4.102m.
Esta expresión se puede obtener hallando el área bajo la curva (trapecio) para el caso general de MRUV con velocidad inicial diferente de cero. Si sustituye la expresión (2) en la (5) se obtiene una nueva expresión para hallar el desplazamiento:  . Esta última expresión puede hallada también, descomponiendo el área bajo la curva en un triangulo y un rectángulo y calculándole área total. Se puede indicar de estudio independiente, hallar otra expresión muy útil para este tipo de movimiento. El estudiante debe despejar el intervalo de tiempo de la ecuación (2) y sustituirla en la ecuación (5).
Obteniendo: 
T2. Construye el gráfico de velocidad en función del tiempo para el auto y la moto para los primeros 40s de iniciado el estudio de sus movimientos.
T3. Un auto viaja a 60 Km/h y al ver a un peatón cruzando la calle y pisa los frenos deteniéndose con un valor de aceleración de -7m/s2. ¿Qué distancia recorrió el auto?
Se debe analizar los parámetros de que depende la distancia de frenado y la importancia que esto tiene para la seguridad vial, en cuanto a excesos de velocidades y mantener la distancia entre vehículos.
T1. Movimientos rectilíneos con aceleración constante de partículas cargadas. Un electrón parte del reposo desde el cátodo y se desplaza 1,4cm hasta el ánodo en un tubo de rayos catódicos. Si al llegar al ánodo el valor de su velocidad es de 5.106m/s, determina la aceleración del electrón.
 |
(2)
|
Para
hallar el desplazamiento de la moto debemos tener en cuenta que la velocidad
varía linealmente con el tiempo y en general el desplazamiento para un
movimiento rectilíneo es:  (3). (3).
Teniendo
en cuenta que en el gráfico de valor de velocidad en función del tiempo, el área
bajo la curva es numéricamente al desplazamiento realizado, podemos encontrar la
solución
Si
calculamos la velocidad media en este movimiento obtenemos que es igual a la
semisuma de los valores inicial y final de velocidad en el intervalo dado.
 (4) entonces el desplazamiento puede expresarse como:
(El
profesor debe saber que si somos consecuente con las cifras significativas del
problema el resultado debe expresarse como, 2,4.102m.
la ecuación (5).
Obteniendo: 
MOVIMIENTOS RECTILÍNEOS
UNIFORMEMENTE VARIADOS
OBJETIVOS
Ilustrar mediante ejemplos de la vida cotidiana
los siguientes conceptos: velocidad media, rapidez, velocidad instantánea,
aceleración.
·
Resolver
problemas de la vida sobre el movimiento rectilíneo uniformemente variado para
determinar la posición, velocidad, desplazamiento, aceleración, en cualquier
instante de tiempo.
·
Ideas esenciales y algunas consideraciones
generales
¿Cómo caracterizar la rapidez a la que varía la
velocidad de un sistema?
T1. Un policía de tráfico arranca su moto al
observar que un auto transita frente a él a una rapidez constante de 98 Km/h.
A los 20s de iniciado su movimiento la moto tiene igual valor de velocidad
que el auto. a) ¿Cómo caracterizar las variaciones de velocidad de la moto?
b) Determina la distancia recorrida por la moto cuando su velocidad (valor)
se iguala a la del auto. c) ¿Cuáles son las principales suposiciones que
realizaste para solucionar este problema?
CM: Al tratarse de dos movimientos en una sola
dimensión, seleccionamos un eje de coordenadas y lo orientamos en la
dirección y sentido del movimiento. Nuestro cuerpo de referencia, es un punto
en la vía donde se encuentran inicialmente los dos cuerpos.
El policía inicia su movimiento en el instante
que el auto pasa frente a él. El valor de la velocidad de la moto comienza a
aumentar en el transcurso del tiempo. ¿Cómo caracterizar las variaciones de
velocidad de la moto en un intervalo de tiempo?
Para describir la rapidez a la que cambia de
posición un cuerpo, se introdujo el concepto de velocidad y el valor de
velocidad media se determinaba por el cociente entre el desplazamiento y el
intervalo de tiempo determinado. Siguiendo esta línea de razonamiento
(analogía), el profesor debe propiciar que los estudiantes que los estudiantes
propongan una magnitud que caracterice en este caso, las variaciones de la
velocidad en un intervalo de tiempo.
La aceleración es la magnitud física
vectorial que caracteriza las variaciones de la velocidad de un sistema en un
intervalo de tiempo.
La aceleración media se puede determinarse como
el cociente entre la variación de la velocidad y el intervalo de tiempo
correspondiente:
Podemos realizar la suposición de que la
moto varía su velocidad uniformemente en el tiempo, al igual que varía la
posición en un MRU. Por tanto las variaciones de la velocidad son iguales en
cualesquiera iguales intervalos de tiempo. Esto significa que la aceleración
media es constante. Este tipo de movimiento recibe el nombre de movimiento
rectilíneo uniformemente variado.
En el movimiento rectilíneo uniformemente
variado el cuerpo realiza iguales variaciones de velocidad en iguales
intervalos de tiempo.
En este movimiento la aceleración es constante.
(La aceleración media es igual a la aceleración
instantánea en el M.R.U.V.)
El valor de la aceleración de la moto la podemos
determinar
Importante en el análisis de unidades, definir la
unidad de aceleración en el SI.
La velocidad instantánea de la moto para
cualquier instante de tiempo puede expresarse de la manera siguiente:
|
Para hallar el
desplazamiento de la moto debemos tener en cuenta que la velocidad varía
linealmente con el tiempo y en general el desplazamiento para un movimiento
rectilíneo es:
(3).
Teniendo en cuenta que en el gráfico de valor
de velocidad en función del tiempo, el área bajo la curva es numéricamente
al desplazamiento realizado, podemos encontrar la solución
Si calculamos la velocidad media en este
movimiento obtenemos que es igual a la semisuma de los valores inicial y
final de velocidad en el intervalo dado.
(4) entonces el desplazamiento puede expresarse
como:
(El profesor debe saber que si somos
consecuente con las cifras significativas del problema el resultado debe
expresarse como, 2,4.102m.
Esta expresión se puede obtener hallando el
área bajo la curva (trapecio) para el caso general de MRUV con velocidad
inicial diferente de cero. Si sustituye la expresión (2) en la (5) se
obtiene una nueva expresión para hallar el desplazamiento:
. Esta última expresión puede hallada también,
descomponiendo el área bajo la curva en un triangulo y un rectángulo y
calculándole área total. Se puede indicar de estudio independiente, hallar
otra expresión muy útil para este tipo de movimiento. El estudiante debe
despejar el intervalo de tiempo de la ecuación (2) y sustituirla en la
ecuación (5).
Obteniendo:
T2. Construye el gráfico de velocidad en
función del tiempo para el auto y la moto para los primeros 40s de iniciado
el estudio de sus movimientos.
T3. Un auto viaja a 60 Km/h y al ver a un
peatón cruzando la calle y pisa los frenos deteniéndose con un valor de
aceleración de -7m/s2. ¿Qué distancia recorrió el auto?
Se debe analizar los parámetros de que depende
la distancia de frenado y la importancia que esto tiene para la seguridad
vial, en cuanto a excesos de velocidades y mantener la distancia entre
vehículos.
T1. Movimientos rectilíneos con aceleración
constante de partículas cargadas.
Un electrón parte del reposo
desde el cátodo y se desplaza 1,4cm hasta el ánodo en un tubo de rayos
catódicos. Si al llegar al ánodo el valor de su velocidad es de 5.106m/s,
determina la aceleración del electrón.
Tabla de conversiones :
CONVERSIONES
MASA
1 lbm = 0, 4536 kg
1 g = 10-3 kg = 6.85 x 10-3slug
1 Kg = 103g = 6.85 x 10-1 slug
1 slug = 1.46 x 104g = 14.6 Kg
1 Tonelada métrica= 1000 Kg
1 Slug = 32.174 Lbm
LONGITUD
1 Cm= 10-2m = 0.394 pulgadas
1 m =10-3 Km =3.28 pies =39.4 pulgadas
1 Km=103m =0.62 millas
1 pulgada = 2.54 cm = 2.54 x 10-2m
1 pie = 12 pulgadas = 30.48 cm = 0.3048 m
1 milla = 5280 pies = 1609 m = 1.609Km
1 yarda = 0.9144m
VOLUMEN
1 litro = 103cm3 = 10-3m3 = 1.056 cuartos = 0.264 galones
1 pulgada cúbica =5.79x 104pies cúbicos= 16.4 cm3=1.64x 105m3
1 pie cúbico= 1728 pulgadas cúbicas=7.48galones=0.0283m3= 28.3 litros
1 cuarto= 2 pintas= 946.5 cm3= 0.947 litros
1 galón = 4 cuartos= 231 pulgadas cúbicas= 3.785litros.
TIEMPO
1h= 60min=3600seg
1 día=24h=1440min=8.64 x 104seg
1 año= 365 días=8.76 x 103h= 5.26 x 105min
Elaborador por: Prof. Ávila Charlie
MEDIDAS LINEALES :
1mm= 0.001m
1 cm= 0.01m= 10mm
1Dcm=0.1m=10cm
1deca=10m
1 hectom=100m=1 hectárea
1 km=1000m
1 Miriam=10000m
1 yarda= 0.9144m
Medidas de Capacidad
1 Barril = 158,9 litros
1 mililitro= 1 cm3
1000 mililitro= 1 litro= 1 dcm3
1000 litros= 1 Kilolitro= 1m3
1000mm3=1 cm3
1000 cm3=1 Dcm3
1000Dcm3= 1 m3
Medidas de Temperatura
Tf= 9/5 ºC + 32
Tc = 5/9 (ºF-32)
Tk= Tc + 273.16
Medidas de Peso
1 Kg= 1000gr
1 Quintal= 220,46 lb
1 Slug= 14.6 Kg
|
|
EJERCICIOS
DE MOVIMIENTO RECTILINEO UNIFORME
VARIADO ( MRUV )
TEORIA DE GRAFICOS DE MRUV
| la velocidad -ahora variable- ya no se puede homologar a la
velocidad media. Mirá el esquema: en tiempos iguales, aumentos iguales de
velocidad. Los desplazamientos ya no son iguales, dado que a mayor velocidad,
tendremos mayores desplazamientos. |
|
 |
|
|
| La flecha de abajo del ciclista
representa la velocidad. Un gráfico velocidad-tiempo típico de
un MRUV podría ser el siguiente: |
|
|
 |
Una recta oblicua bien puede representar un MRUV. Si la
inclinación es como ésta la llamamos ascendente o creciente y decimos que se
trata de un movimiento de aumento de velocidad; y a la inversa: descendente o
decreciente, que se corresponde con disminuciones de la velocidad. Pero la
inclinación nada nos informa sobre si el móvil avanza o retrocede.
Para saber si el móvil avanza o retrocede
hay que prestar atención al signo de la
velocidad (o sea, gráficamente: si está arriba o abajo del eje
de los tiempos). |
|
|
|
Si la recta fuese horizontal representaría un móvil que no cambia la
velocidad, y en ese caso se trataría de un MRU. Aunque parezca
ridículo también lo incluimos dentro de los MRUV. La
orientación prohibida es la vertical: indicaría que el móvil posee infinitas
velocidades en un mismo instante.
Fijate que la recta no necesariamente pasa por la posición v =
0 en el instante t = 0.
Como ves, la velocidad se comporta en el
MRUV como la posición en el
MRU. Seguro que hay una ecuación
horaria (la llamamos segunda ecuación horaria) que describe
cómo varía la velocidad a través del tiempo:
v = vo + a ( t – to
)
v y t son las variables. Si no
aparecen, fuiste; no hay ecuación horaria. El resto: vo , a y to , son constantes, o sea
números. vo y
to son una
velocidad cualquiera que el móvil tenga y el instante en que la haya tenido (o
sea, se corresponden entre sí). Y a es la magnitud que describe el cambio de
velocidad y se llama aceleración. Justamente, la característica
fundamental del MRUV es a = cte.
Gracias a eso, podemos calcularla como una aceleración media,
am. |
|
las unidades de la aceleración son m/s²o cualquier otra unidad de longitud
sobre cualquier unidad de tiempo al cuadrado
|
| am |
= |
Δv12 |
= |
v2
– v1 |
|
|
|
| Δt12 |
t2
– t1 |
|
CAPACIDAD ELECTRICA Y CONDENSADORES
CAPACIDAD ELECTRICA
En electromagnetismo y electrónica, la capacidad eléctrica, también conocida como capacitancia, es la propiedad que tienen los cuerpos para mantener una carga eléctrica. La capacidad también es una medida de la cantidad de energía eléctrica almacenada para una diferencia de potencial eléctrico dada. El dispositivo más común que almacena energía de esta forma es el condensador. La relación entre la diferencia de potencial (o tensión) existente entre las placas del condensador y la carga eléctrica almacenada en éste, se describe mediante la siguiente expresión matemática:
donde:
 es la capacidad, medida en faradios (en honor al físico experimental Michael Faraday); esta unidad es relativamente grande y suelen utilizarse submúltiplos como el microfaradio o picofaradio. es la capacidad, medida en faradios (en honor al físico experimental Michael Faraday); esta unidad es relativamente grande y suelen utilizarse submúltiplos como el microfaradio o picofaradio.
-
-
Cabe destacar que la capacidad es siempre una cantidad positiva y que depende de la geometría del condensador considerado (de placas paralelas, cilíndrico, esférico). Otro factor del que depende es del dieléctrico que se introduzca entre las dos superficies del condensador. Cuanto mayor sea la constante dieléctrica del material no conductor introducido, mayor es la capacidad.
En la práctica, la dinámica eléctrica del condensador se expresa gracias a la siguiente ecuación diferencial, que se obtiene derivando respecto al tiempo la ecuación anterior.
ENERGIA:
La energía almacenada en un condensador, medida en joules, es igual al trabajo realizado para cargarlo. Consideremos un condensador con una capacidad C, con una carga +q en una placa y -q en la otra. Para mover una pequeña cantidad de carga  desde una placa hacia la otra en sentido contrario a la diferencia de potencial se debe realizar un trabajo desde una placa hacia la otra en sentido contrario a la diferencia de potencial se debe realizar un trabajo 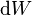 : :
donde
W es el trabajo realizado, medido en julios;
-
-
Es decir, para cargar un condensador hay que realizar un trabajo y parte de este trabajo queda almacenado en forma de energía potencial electrostática. Se puede calcular la energía almacenada en un condensador integrando esta ecuación. Si se comienza con un condensador descargado (q = 0) y se mueven cargas desde una de las placas hacia la otra hasta que adquieran cargas +Q y -Q respectivamente, se debe realizar un trabajo W:
-
Combinando esta expresión con la ecuación de arriba para la capacidad, obtenemos:
-
donde
W es la energía, medida en julios;
-
V es la diferencia de potencial, medido en voltios;
-
AUTOCAPACIDAD:
Usualmente el término capacidad mutua se utiliza como abreviatura del término capacidad entre dos conductores cercanos, como las placas de un condensador. Sin embargo, para un conductor aislado también existe una propiedad llamada auto-capacitancia que es la cantidad de carga eléctrica que debe agregarse a un conductor aislado para aumentar su potencial en un voltio, para así calcular la capacidad eléctrica mediante un condensador paralelo o plano. El punto de referencia teórico para este potencial es una esfera hueca conductora, de radio infinito, centrado en el conductor. Usando este método, la auto-capacitancia de una esfera conductora de radio R está dada por:

Estos son algunos ejemplos de valores de auto-capacitancia:
Para el "plato" de la parte superior de un generador de Van de Graaff, normalmente una esfera de 20 cm de radio: 22.24 pF
El planeta Tierra: unos 710 µF
CONDENSADOR ELECTRICO
Un condensador eléctrico o capacitor es un dispositivo pasivo, utilizado en electricidad y electrónica, capaz de almacenar energía sustentando un campo eléctrico.[1] [2] Está formado por un par de superficies conductoras, generalmente en forma de láminas o placas, en situación de influencia total (esto es, que todas las líneas de campo eléctrico que parten de una van a parar a la otra) separadas por un material dieléctrico o por el vacío. Las placas, sometidas a una diferencia de potencial, adquieren una determinada carga eléctrica, positiva en una de ellas y negativa en la otra, siendo nula la variación de carga total.
Aunque desde el punto de vista físico un condensador no almacena carga ni corriente eléctrica, sino simplemente energía mecánica latente; al ser introducido en un circuito se comporta en la práctica como un elemento "capaz" de almacenar la energía eléctrica que recibe durante el periodo de carga, la misma energía que cede después durante el periodo de descarga.
FUNCIONAMIENTO:
La carga almacenada en una de las placas es proporcional a la diferencia de potencial entre esta placa y la otra, siendo la constante de proporcionalidad la llamada capacidad o capacitancia. En el Sistema internacional de unidades se mide en Faradios (F), siendo 1 faradio la capacidad de un condensador en el que, sometidas sus armaduras a una d.d.p. de 1 voltio, estas adquieren una carga eléctrica de 1 culombio.
La capacidad de 1 faradio es mucho más grande que la de la mayoría de los condensadores, por lo que en la práctica se suele indicar la capacidad en micro- µF = 10-6, nano- nF = 10-9 o pico- pF = 10-12 -faradios. Los condensadores obtenidos a partir de supercondensadores (EDLC) son la excepción. Están hechos de carbón activado para conseguir una gran área relativa y tienen una separación molecular entre las "placas". Así se consiguen capacidades del orden de cientos o miles de faradios. Uno de estos condensadores se incorpora en el reloj Kinetic de Seiko, con una capacidad de 1/3 de Faradio, haciendo innecesaria la pila. También se está utilizando en los prototipos de automóviles eléctricos.
El valor de la capacidad de un condensador viene definido por la siguiente fórmula:
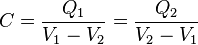
en donde:
 : Capacitancia o capacidad : Capacitancia o capacidad : Carga eléctrica almacenada en la placa 1. : Carga eléctrica almacenada en la placa 1. : Diferencia de potencial entre la placa 1 y la 2. : Diferencia de potencial entre la placa 1 y la 2.
Nótese que en la definición de capacidad es indiferente que se considere la carga de la placa positiva o la de la negativa, ya que

aunque por convenio se suele considerar la carga de la placa positiva.
En cuanto al aspecto constructivo, tanto la forma de las placas o armaduras como la naturaleza del material dieléctrico son sumamente variables. Existen condensadores formados por placas, usualmente de aluminio, separadas por aire, materiales cerámicos, mica, poliéster, papel o por una capa de óxido de aluminio obtenido por medio de la electrólisis.
ENERGIA ALMACENADA:
Cuando aumenta la diferencia de potencial entre sus terminales, el condensador almacena carga eléctrica debido a la presencia de un campo eléctrico en su interior; cuando esta disminuye, el condensador devuelve dicha carga al circuito. Matemáticamente se puede obtener que la energía  , almacenada por un condensador con capacidad , almacenada por un condensador con capacidad  , que es conectado a una diferencia de potencial , que es conectado a una diferencia de potencial  , viene dada por: , viene dada por:
Fórmula para cualesquiera valores de tensión inicial y tensión final:  Donde Donde  es la carga inicial. es la carga inicial. 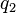 es la carga final. es la carga final. 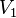 es la tensión inicial. es la tensión inicial. 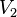 es la tensión final. es la tensión final.
Este hecho es aprovechado para la fabricación de memorias, en las que se aprovecha la capacidad que aparece entre la puerta y el canal de los transistores MOS para ahorrar componentes.
CARAGA Y DESCARGA:
Al conectar un condensador en un circuito, la corriente empieza a circular por el mismo. A la vez, el condensador va acumulando carga entre sus placas. Cuando el condensador se encuentra totalmente cargado, deja de circular corriente por el circuito. Si se quita la fuente y se coloca el condensador y la resistencia en paralelo, la carga empieza a fluir de una de las placas del condensador a la otra a través de la resistencia, hasta que la carga es nula en las dos placas. En este caso, la corriente circulará en sentido contrario al que circulaba mientras el condensador se estaba cargando.
- Carga
-
 
- Descarga
-
 
Donde:
- V(t) es la tensión en el condensador.
- Vi es la tensión o diferencia de potencial eléctrico inicial (t=0) entre las placas del condensador.
- Vf es la tensión o diferencia de potencial eléctrico final (a régimen estacionario t>=4RC) entre las placas del condensador.
- I(t) la intensidad de corriente que circula por el circuito.
- RC es la capacitancia del condensador en faradios multiplicada por la resistencia del circuito en Ohmios, llamada constante de tiempo.
EN CORRIENTE ALTERNA:
En CA, un condensador ideal ofrece una resistencia al paso de la corriente que recibe el nombre de reactancia capacitiva, XC, cuyo valor viene dado por la inversa del producto de la pulsación ( ) por la capacidad, C: ) por la capacidad, C:
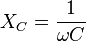
Si la pulsación se expresa en radianes por segundo (rad/s) y la capacidad en faradios (F), la reactancia resultará en ohmios.
De acuerdo con la ley de Ohm, la corriente alterna que circule por el condensador se adelantará 90º (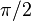 ) respecto a la tensión aplicada. ) respecto a la tensión aplicada.
ASOCIACIONES DE CONDENSADORES:
Los condensadores pueden asociarse en serie, paralelo o de forma mixta. En estos casos, la capacidad equivalente resulta ser para la asociación en serie:
y para la asociación en paralelo:
Es decir, el sumatorio de todas las capacidades de los condensadores conectados en paralelo.
Es fácil demostrar estas dos expresiones, para la primera solo hay que tener en cuenta que la carga almacenada en las placas es la misma en ambos condensadores (se tiene que inducir la misma cantidad de carga entre las placas y por tanto cambia la diferencia de potencial para mantener la capacitancia de cada uno), y por otro lado en la asociación en "paralelo", se tiene que la diferencia de potencial entre ambas placas tiene que ser la misma (debido al modo en el que están conectados), así que cambiará la cantidad de carga. Como esta se encuentra en el numerador (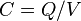 ) la suma de capacidades será simplemente la suma algebraica. ) la suma de capacidades será simplemente la suma algebraica.
CONDENSADORES VARIABLES:
Los condensadores pueden asociarse en serie, paralelo o de forma mixta. En estos casos, la capacidad equivalente resulta ser para la asociación en serie:
y para la asociación en paralelo:
Es decir, el sumatorio de todas las capacidades de los condensadores conectados en paralelo.
Es fácil demostrar estas dos expresiones, para la primera solo hay que tener en cuenta que la carga almacenada en las placas es la misma en ambos condensadores (se tiene que inducir la misma cantidad de carga entre las placas y por tanto cambia la diferencia de potencial para mantener la capacitancia de cada uno), y por otro lado en la asociación en "paralelo", se tiene que la diferencia de potencial entre ambas placas tiene que ser la misma (debido al modo en el que están conectados), así que cambiará la cantidad de carga. Como esta se encuentra en el numerador (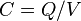 ) la suma de capacidades será simplemente la suma algebraica. ) la suma de capacidades será simplemente la suma algebraica.
TIPOS DE DIELCTRICOS UTILIZADOS EN CONDENSADORES:
Condensadores de aire. Se trata de condensadores, normalmente de placas paralelas, con dieléctrico de aire y encapsulados en vidrio. Como la permitividad eléctrica relativa es la unidad, sólo permite valores de capacidad muy pequeños. Se utilizó en radio y radar, pues carecen de pérdidas y polarización en el dieléctrico, funcionando bien a frecuencias elevadas.
Condensadores de mica. La mica posee varias propiedades que la hacen adecuada para dieléctrico de condensadores: bajas pérdidas, exfoliación en láminas finas, soporta altas temperaturas y no se degrada por oxidación o con la humedad. Sobre una cara de la lámina de mica se deposita aluminio, que forma una armadura. Se apilan varias de estas láminas, soldando los extremos alternativamente a cada uno de los terminales. Estos condensadores funcionan bien en altas frecuencias y soportan tensiones elevadas, pero son caros y se ven gradualmente sustituidos por otros tipos.
Condensadores de papel. El dieléctrico es papel parafinado, baquelizado o sometido a algún otro tratamiento que reduce su higroscopia y aumenta el aislamiento. Se apilan dos cintas de papel, una de aluminio, otras dos de papel y otra de aluminio y se enrollan en espiral. Las cintas de aluminio constituyen las dos armaduras, que se conectan a sendos terminales. Se utilizan dos cintas de papel para evitar los poros que pueden presentar.
- Condensadores autorregenerables. Los condensadores de papel tienen aplicaciones en ambientes industriales. Los condensadores autorregenerables son condensadores de papel, pero la armadura se realiza depositando aluminio sobre el papel. Ante una situación de sobrecarga que supere la rigidez dieléctrica del dieléctrico, el papel se rompe en algún punto, produciéndose un cortocircuito entre las armaduras, pero este corto provoca una alta densidad de corriente por las armaduras en la zona de la rotura. Esta corriente funde la fina capa de aluminio que rodea al cortocircuito, restableciendo el aislamiento entre las armaduras.
Condensadores electrolíticos. Es un tipo de condensador que utiliza un electrolito, como su primera armadura, la cual actúa como cátodo. Con la tensión adecuada, el electrolito deposita una capa aislante (la cual es en general una capa muy fina de óxido de aluminio) sobre la segunda armadura o cuba (ánodo), consiguiendo así capacidades muy elevadas. Son inadecuados para funcionar con corriente alterna. La polarización inversa destruye el óxido, produciendo un cortocircuito entre el electrolito y la cuba, aumentando la temperatura, y por tanto, arde o estalla el condensador consecuentemente. Existen varios tipos, según su segunda armadura y electrolito empleados:
- Condensadores de aluminio. Es el tipo normal. La cuba es de aluminio y el electrolito una disolución de ácido bórico. Funciona bien a bajas frecuencias, pero presenta pérdidas grandes a frecuencias medias y altas. Se emplea en fuentes de alimentación y equipos de audio. Muy utilizado en fuentes de alimentación conmutadas.
- Condensadores de tantalio (tántalos). Es otro condensador electrolítico, pero emplea tantalio en lugar de aluminio. Consigue corrientes de pérdidas bajas, mucho menores que en los condensadores de aluminio. Suelen tener mejor relación capacidad/volumen.
- Condensadores bipolares (para corriente alterna). Están formados por dos condensadores electrolíticos en serie inversa, utilizados en caso de que la corriente pueda invertirse. Son inservibles para altas frecuencias.
Condensadores de poliéster o Mylar. Está formado por láminas delgadas de poliéster sobre las que se deposita aluminio, que forma las armaduras. Se apilan estas láminas y se conectan por los extremos. Del mismo modo, también se encuentran condensadores de policarbonato y polipropileno.
Condensadores de poliestireno también conocidos comúnmente como Styroflex (marca registrada de Siemens). Otro tipo de condensadores de plástico, muy utilizado en radio, por disponer de coeficiente de temperatura inverso a las bobinas de sintonía, logrando de este modo estabilidad en los circuitos resonantes.
Condensadores cerámicos. Utiliza cerámicas de varios tipos para formar el dieléctrico. Existen diferentes tipos formados por una sola lámina de dieléctrico, pero también los hay formados por láminas apiladas. Dependiendo del tipo, funcionan a distintas frecuencias, llegando hasta las microondas.
Condensadores síncronos. Es un motor síncrono que se comporta como un condensador.
Dieléctrico variable. Este tipo de condensador tiene una armadura móvil que gira en torno a un eje, permitiendo que se introduzca más o menos dentro de la otra. El perfil de la armadura suele ser tal que la variación de capacidad es proporcional al logaritmo del ángulo que gira el eje.
- Condensadores de ajuste. Son tipos especiales de condensadores variables. Las armaduras son semicirculares, pudiendo girar una de ellas en torno al centro, variando así la capacidad. Otro tipo se basa en acercar las armaduras, mediante un tornillo que las aprieta.
USOS:
Los condensadores suelen usarse para:
Baterías, por su cualidad de almacenar energía.
Memorias, por la misma cualidad.
Filtros.
-
Adaptación de impedancias, haciéndolas resonar a una frecuencia dada con otros componentes.
-
-
El flash de las cámaras fotográficas.
Tubos fluorescentes.
-
-
Mantener corriente en el circuito y evitar caídas de tensión.
Condensador
|
|---|
 Varios tipos de condensadores Varios tipos de condensadores
|
Tipo |
|
|---|
Principio de funcionamiento |
|
|---|
Fecha de invención |
|
|---|
Primera producción |
|
|---|
Símbolo electrónico |
|---|
|
|
Configuración |
En condensadores electrolíticos: negativo y positivo; en cerámicos: no presentan polaridad
|
|---|
Condensadores electrolíticos axiales.
Condensador variable de una vieja radio AM
|
|
|
No hay comentarios.:
Publicar un comentario